Getting Started

This page details how to get started with FreeVirgil.

Installation (Python)

Requirements:

• Python3

Install by exectuting:

pip install git+https://github.com/zacc23/freevirgil.git

or

git clone https://github.com/zacc23/freevirgil.git
cd freevirgil
pip install .

Installation (C++)

Requirements:

• CERN ROOT

For getting N spins:

git clone https://github.com/zacc23/OhMyGodWhatHappenedToVirgil.git
cd OhMyGodWhatHappenedToVirgil
c++ examples/getN.cpp -I. -Ofast -Wall -Wpedantic -o getN

For plotting:

git clone https://github.com/zacc23/OhMyGodWhatHappenedToVirgil.git
cd OhMyGodWhatHappenedToVirgil
c++ examples/plot.cpp -Ofast -I. $(root-config --cflags --libs) -Wall -Wpedantic -o plot

References

Gibbs Distribution

Probability: \(P(\alpha) = e^{-E(\alpha)/kT}\) with Boltzmann constant, \(k = 1.38064852 \times 10^{-23} J/K\) and a temperature T in Kelvin. This gives the probability of observing \(\alpha\), a particular spin.

Ising Hamiltonian

Energy: \(\displaystyle\hat{H}' = \frac{\hat{H}}{k} = -\frac{J}{k}\sum_{<ij>} s_is_j + \tfrac{\mu}{k}\sum_i s_i\). This gives the energy where \(s_i = 1\) if the \(i^{th}\) spin is up and \(s_i = -1\) if it is down.

Magnetization: \(M(\alpha) = N_{\text{up}}(\alpha) - N_{\text{down}}(\alpha)\). The sum of spins pointing up, minus those pointing down.

Averages

\(\left<M\right> = \sum_\alpha M(\alpha)P(\alpha)\). The average magnetization, which is found through the sum of each magnetism with its respective probability.

\(\left<E\right> = \sum_\alpha E(\alpha)P(\alpha)\). The average energy, which is found through the sum of each energy with its respective probability.

Examples

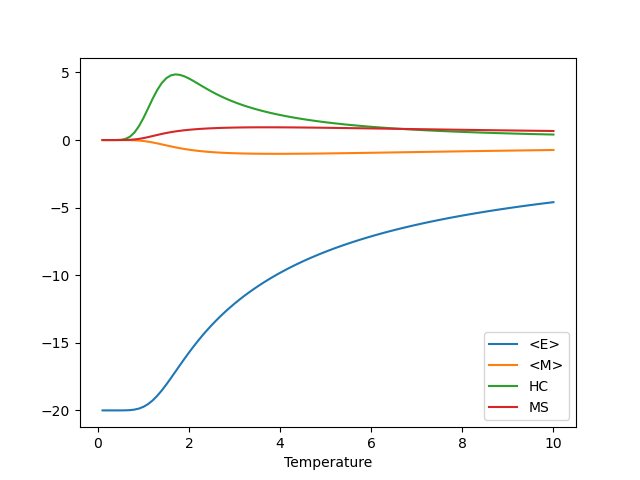
Plot (Python)

import math
import freevirgil as fv
from matplotlib import pyplot as plt

spin = fv.spin_conf(N=10)
ham = fv.hamiltonian(J=-2, mu=1.1)

irange = 100
T = [0] * irange
E = [0] * irange
M = [0] * irange
HC = [0] * irange
MS = [0] * irange

for i in range(0, irange):

    T[i] = 0.1 * (i + 1)
    E[i], M[i], HC[i], MS[i] = ham.avg(spin, T[i])
    
plt.figure(num = 0, dpi = 100)
plt.plot(T, E, label="<E>")
plt.plot(T, M, label="<M>")
plt.plot(T, HC,  label="HC")
plt.plot(T, MS, label="MS")
plt.legend()
plt.xlabel("Temperature")

plt.savefig("plot.png")

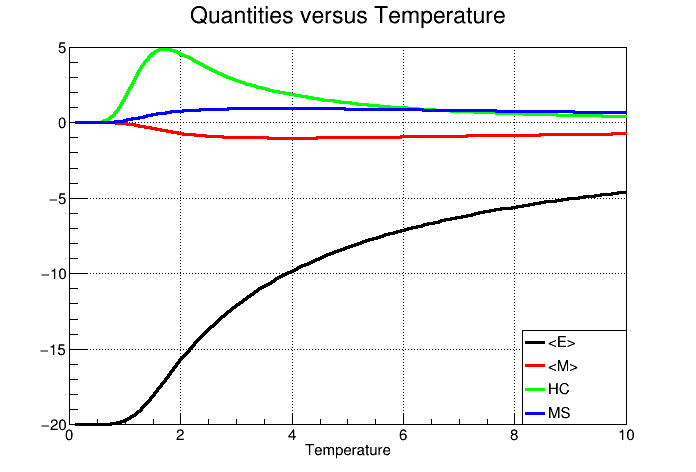
Plot (C++)

/*
graph program for the freevirgil package.
*/

#include <TCanvas.h>
#include <TFrame.h>
#include <TAxis.h>
#include <TGraph.h>
#include <TLegend.h>

#include <iostream>
#include "spin_conf.h"
#include "hamiltonian.h"

int main()
{
	TCanvas *c1 = new TCanvas("c1", "Plot of Quantities versus Temperature", 
		200, 10, 700, 500);
	c1->SetGrid();
        c1->GetFrame()->SetBorderSize(12);

	// N = 10
        spin_conf spin(10);
        // J = -2, mu = 1.1
        hamiltonian ham(-2, 1.1);

	const int irange = 100;
        double T[irange],
		E[irange],
		M[irange], 
		HC[irange],
	 	MS[irange];

        for (int i = 0; i < irange; i++)
        {
		// start at .1, increment by .1 until end
                T[i] = 0.1 * (i + 1);
		//cout << T[i] << endl;
                ham.avg(spin, T[i], E[i], M[i], HC[i], MS[i]);
		//cout << T[i] << ' ' << E[i] << ' ' << M[i] << 
		//	' ' << HC[i] << ' ' << MS[i] << endl;
        }

	TGraph *EvT = new TGraph(irange, T, E);
	TGraph *MvT = new TGraph(irange, T, M);
        TGraph *HCvT = new TGraph(irange, T, HC);
        TGraph *MSvT = new TGraph(irange, T, MS);
	TLegend *leg = new TLegend(0.75, 0.1, 0.9, 0.3);

	EvT->SetTitle("Quantities versus Temperature");
	EvT->GetXaxis()->SetTitle("Temperature");
        EvT->GetXaxis()->CenterTitle(true);
	EvT->GetXaxis()->SetRangeUser(0, 10);
        EvT->GetYaxis()->SetRangeUser(-20, 5);
	EvT->SetLineWidth(3);
	EvT->SetLineColor(1);
	EvT->Draw("AC");
	
	MvT->SetLineWidth(3);
        MvT->SetLineColor(2);
        MvT->Draw("CSame");

	HCvT->SetLineWidth(3);
        HCvT->SetLineColor(3);
        HCvT->Draw("CSame");

	MSvT->SetLineWidth(3);
        MSvT->SetLineColor(4);
        MSvT->Draw("CSame");

	//leg->SetHeader("The Legend Title");
	leg->AddEntry(EvT, "<E>", "l");
	leg->AddEntry(MvT, "<M>", "l");
	leg->AddEntry(HCvT, "HC", "l");
	leg->AddEntry(MSvT, "MS", "l");
	leg->Draw();

	c1->Update();
        c1->Print("plot.pdf");
        c1->Print("plot.png");
	
	return 0;
}

Speed

Tested by prefacing the execution command with time (with 10 sites)

Python (plot.py)

0m02.72s real     0m02.61s user     0m00.08s system

C++ (plot.cpp)

• Default optimization

0m00.71s real     0m00.58s user     0m00.13s system

• With g++ -Ofast flag

0m00.54s real     0m00.43s user     0m00.12s system